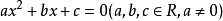已知关于x的方程x的平方-(2k+1)x+4(k-1/2)=0 (1)求证：这个方程总有两个实数根

已知关于x的方程x的平方-(2k+1)x+4(k-1/2)=0 (1)求证：这个方程总有两个实数根

问题补充说明：（2）若等腰三角形ABC的一边长a=4，另两边b、c恰好是这个方程的两个实数根，求△ABC的周长。要详细过程。

1.

x²-(2k+1)x+4(k-1/2)=0

△=(2k+1)²-16(k-1/2)

=4k²-12k+9

=4(k²-3k+9/4)

=4(k-3/2)²≥0

∴这个方程总有两个实数根

2.

①若a是底边长，则b=c

即△=4(k-9/2来自)²=0，k=3/2，

根据根360问答与系数关系(韦达定理)得

b+c=2k+1=4=a，所以不满足（因为b+c>a）

②若a是腰长，设令一腰为b=a=4

把一根4代入方程，得k=5/2

根据根与系数关系(韦达定理)得

b+c急降名握差圆衡官杀=2k+1=6>a，

c=2

C=a+b+c=10