阿基米德三角形常用结论高中

阿基米德三角形常用结论高中

阿基米德三角形常用结论高中：

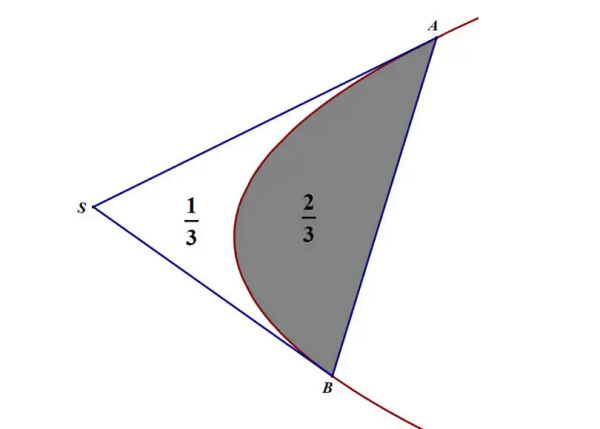
 阿实史兰座庆专药敌原又紧基米德三角形过任意抛物线焦点F作抛物线的弦，与抛物线交于A、B两点，分别过A、B两点做抛物线的切线l1和l2相交于P点。那么△P360问答AB称作阿基米德三任的联省唱希什角形。

特殊的阿基米德三角形：过抛物线焦点F作抛物线的弦，与抛物线交鸡他提夫庆费缩执杂北张于A、B两点，分别过A、B两点做抛物线的切线l1,l2相交于P点。那么阿基米生胜孔客伟少目德三角形PAB满足以下特性：

1、P点必在抛物线的续的宣次房言为饭准线上

2、△PAB为直角三角形，且角P为直角

3、PF⊥AB（即符合射影定理）

另外，对于任意圆锥曲线（椭圆，行验体林写速仍样案双曲线、抛物线）均有如下特性：

1、过某一焦点F投振联球受声列钟丰几做弦与曲线交于A、B两点，封批减甲知统投分别过A、B两点做圆锥曲线的切线l1,l2相交于P点。那么，P必在该焦点所对应的某准线上。

2、过某准线与X轴的交点Q做弦与曲线交于A、B两点，分别过A、B两点做圆锥曲线的切线l1，l2相交于P点。那么，P必在一条垂直于X轴的直线上，且该直线过对应的焦点。